Das Legespiel Pythagoras hilft die abstrakte Gleichung des "Satz des Pythagoras" zu verstehen und zu begreifen.
Die Spielideen lassen die Kinder außerdem entdecken, wie aus einer geometrischen Form eine andere entsteht, und welche Gemeinsamkeiten die Flächen haben. So wird das Verständnis für geometrische Flächen gefördert.
Mit der neu überarbeiteten und an die Bausteine angepassten Arbeitskartei erarbeiten Kinder handlungsorientiert und selbständig den Satz des Pythagoras, überprüfen dessen Richtigkeit, lernen grundlegende geometrische Begriffe kennen und experimentieren mit der Raumlage geometrischer Formen.
Das Set "Legespiel und Experimente zum Satz des Pythagoras" ist in der SBA mit dem Titel "Legespiel Pythagoras" mit der Nr. 200.652 gelistet und wird als SBA-Bestellung immer auf Kunststoff-Karten geliefert.
Bild 1
Das Lernmaterial-Set besteht aus:
102 Teile aus Holz im Leinenbeutel
Arbeitskartei (ca. A5) mit 13 beidseitig bedruckte Auftragskarten mit 23 Arbeitsaufträgen und Lösungsfotos, zwei Karten mit einem Überblick zu geometrischen Figuren, Anleitung für "Legespiel des Pythagoras", eine Infokarte und eine Titelkarte.
Lieferform:
102 Teile aus Holz im Leinenbeutel
9 A4-Blätter, z.T. beidseitig bedruckt
Bild 2 une 3
Anwendung:
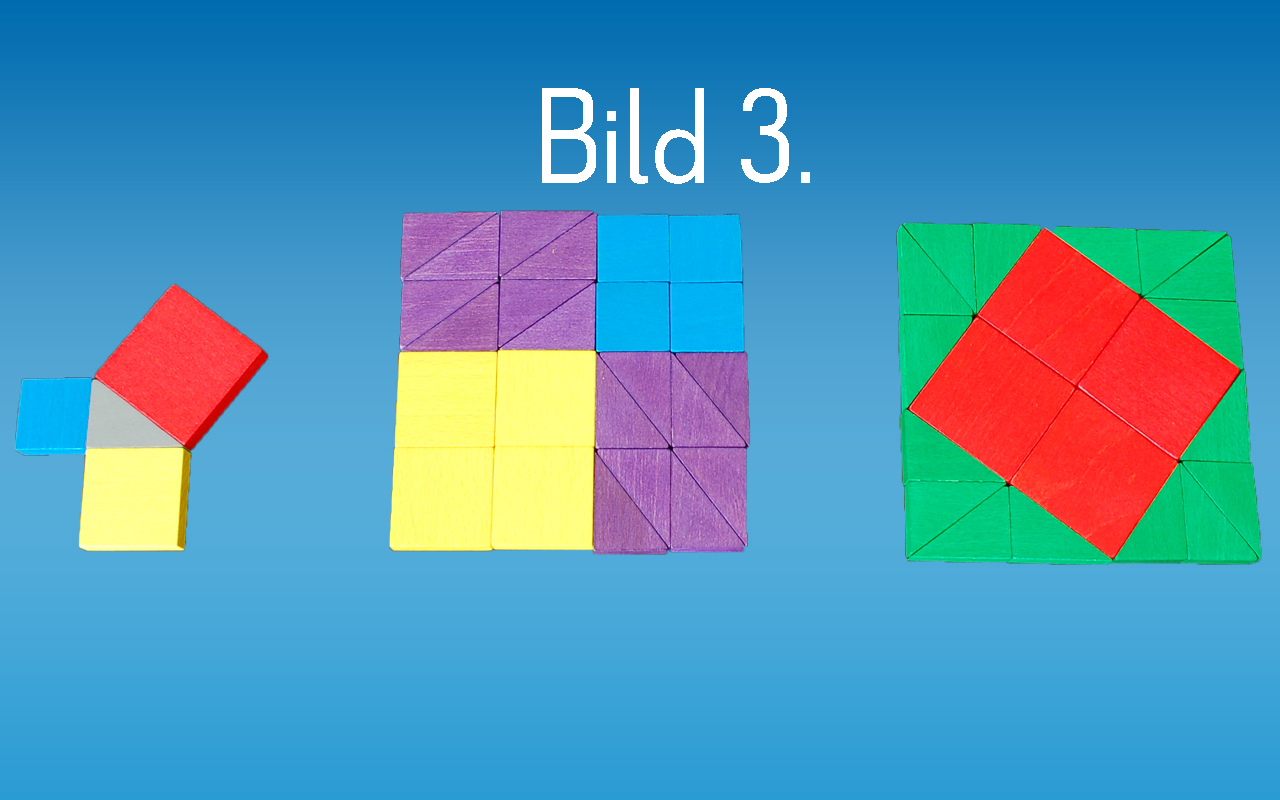
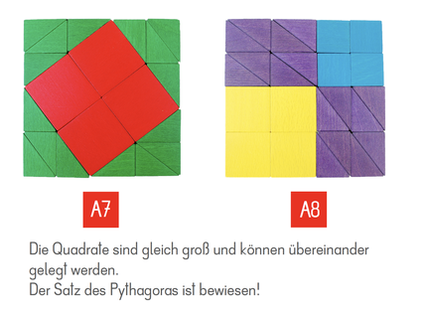
Die Formel a² + b² = c² kann mit den Quadraten und Dreiecken nachgelegt werden, womit bewiesen werden kann, dass a² + b² auch wirklich die gleiche Fläche wie c² erreicht. Sichtbar gemacht, ist der Satz des Pythagoras gut zu verstehen, glaubhaft und nachvollziehbar.
Bild 4
Bei diesem Experiment können die Lernenden ausprobieren, ob sich mit den Quadraten der Flächen a² und b² die Fläche c² abdecken lässt.
Die Abbildung der Gleichung wird schrittweise vom kleinsten Format in das jeweils größere Format gelegt. Für die größeren Formate sind die Kinder aufgefordert zu überlegen wie sie z.B. die kleinen Dreiecke zu einem großen Dreieck aneinanderlegen können und wie Sie die Farben den Flächen zuordnen um die Übersicht zu bewahren.
Zum Schluss werde die Flächen a² und b² zusammengefügt, um die Fläche c² abzudecken - oder umgekehrt... - und das gelingt auf den Millimeter genau.
Bild 5
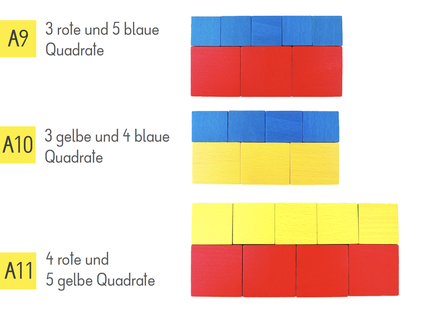
Es können auch andere geometrische Formen aus den Puzzelteilen gelegt werden. Hier ist es einfacher wenn man am Anfang die Teile sortiert und die Kinder z.B. als erstes nur Dreiecke zum Legen nehmen.
Wenn einige Formen entdeckt wurden, können die Dreiecke und Quadrate gemischt werden. Welche Formen lassen sich nun legen? Nach diesem Entdecken können die Formen gezeichnet und benannt werden.
Hier sind einige Beispiele für Formen, aber es gibt sicher noch viel mehr Möglichkeiten eine Form zu legen und auch noch mehr Formen zu entdecken.
Bild 6
Spielempfehlung zum Legespiel "Lehrsatz des Pythagoras":
Vorbereitung:
Jeder Spieler erhält von jeder Farbe drei Spielsteine. Die restlichen Teile werden in einem Säckchen gut erreichbar für alle Spieler abgelegt. Nun wird in die Mitte ein graues Dreieck und die passenden drei Quadrate angelegt.
Die Formen umfassen die Quadrate in drei unterschiedlichen Größen und Farben sowie drei rechtwinkelige Dreiecke in den Farben violett, grün und grau.
Bild 7
Die Spielzüge:
Die Spielenden setzen reihum jeweils einen Spielstein. Jeder gespielte Spielstein muss so platziert werden, dass eine seiner Seiten dieselbe Länge hat wie die Form, an die es gelegt wird.
Es müssen immer abwechselnde Formen angelegt werden: Quadrat an Rechteck oder Rechteck an Quadrat.
Kann jemand kein Teil passend anlegen, so muss ausgesetzt und ein Spielstein aus dem Säckchen gezogen werden.
Bild 8
Ist kein Teil mehr im Säckchen oder hat jemand seinen letzten Spielstein angelegt, so endet das Spiel.
Gewonnen hat der Spieler, der nach Spielende die wenigsten oder keine Spielsteine übrig hat.
Das Legespiel "Der Satz des Pythagoras" ist ein kooperatives Spiel, wo in der Zusammenarbeit aller Spielenden ein Gesamtbild - ein Pythagoras-Mandala - entsteht.
Das Spiel kann mit mehreren Spielern oder Solitaire gespielt werden.